In my first article on Survival Analysis, I introduced the concept of a survival function and how we can use this to compare different demographics in the case of churn. Here the mode of transport was used to compare churn rates for employees at a fictitious company. It was evident that cyclists were much more likely to “survive” (at least risk of turnover) compared to their peers who drove by car. An important point that was omitted from the previous article, however, and is the subject of this article, is the notion of censoring in Survival Analysis.
What is censoring?
The notion of censoring is fundamental to survival analysis and is used when computing our survival functions (more on that in the next part of the series). But what do I mean by censoring? Strictly speaking, censoring is a condition when only part of the observation or measurement is known. That is the ability to take into account missing data, whereby the time to event is not observed.
For example, death in office of a president, or someone leaving a medical study before the study formally concludes. In the case of the latter, you can see this is really important for the analysis in medical trials, but in both cases the underlying principle is the same – we made some observations until a given time, but we cannot measure the event. If a president dies after one year in office, how can we possibly know that they would have served two terms?
Left and right censoring in Survival Analysis
There are different types of censoring, two commonly discussed ones are left and right censoring (two others that come to mind are interval censoring and random censoring, but are not discussed here).
- Left censoring is when the event has occurred before the data is collected (or study has started) – that is we only know the upper bound of the time. For example, in a medical study someone dies before the drug trial begins (which is normally not considered).
- Whereas, right censoring is when only a lower limit of the time is known, for example, if a subject leaves a study before the end, or the study ends before the event occurs.
You can think of this as events that happened to the left of time (in the past) are left censored, and events that may happen to the right of time (in the future) are right censored.
In the case of turnover, we are only considering right censoring, where a person may leave at some point in the future, but we don’t know when they will (if at all). Hopefully, the diagram below will help demonstrate this.
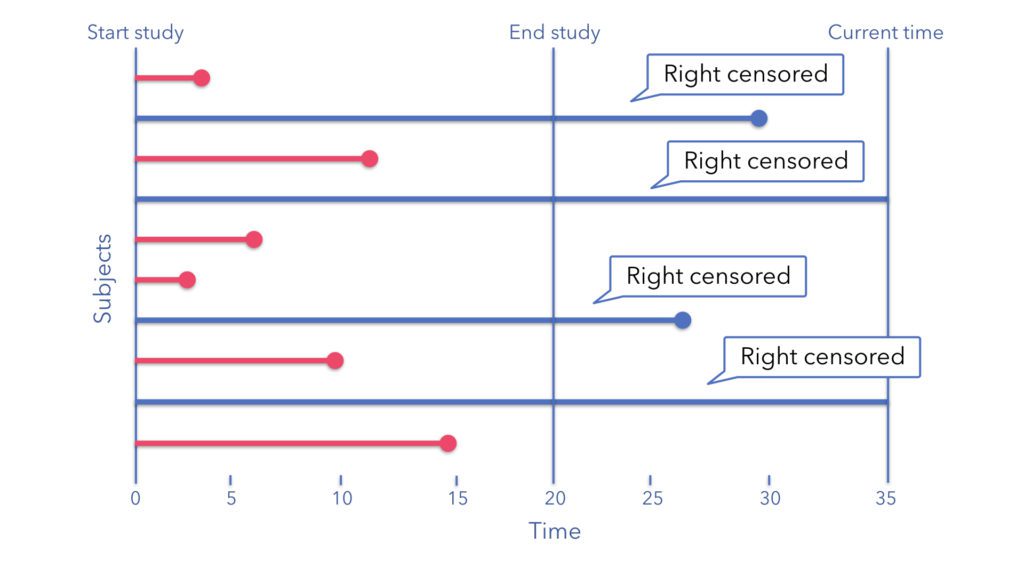
Example of censoring: medical study
In the above example, we have 10 subjects in a medical study that begins at time t=0 and ends at time t=20 (don’t worry about units in this example, you can imagine weeks, months, years if it helps). Each subject is recorded until either the event happens (circle) or the end of the study is reached (the black vertical line at t=20).
As you can see we observe the event during the study for the red subjects, and the blue lines represent participants that no event occurred during the study period. Notice that some of the blue lines do end before the current time but occur after the end of the study period, and this is the critical thing, they are right-censored! If we did not include this into our analysis we would be underestimating the true average for our subjects.
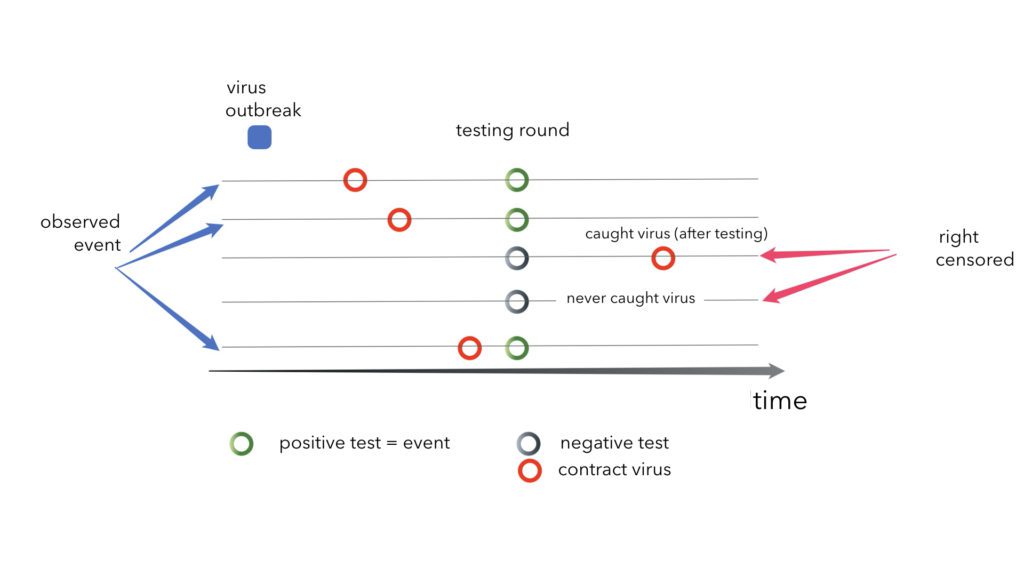
Example of censoring: virus testing
Another example, which is much more fitting in today’s climate, is one that concerns virus testing. Let us imagine that some proportion of the population has been exposed to a virus and individuals are tested at a given point in time to see whether they have the virus or not. We will assume that these tests are
- unrealistically accurate
- produce no false positives or negatives
- therefore anyone who tests positive has the virus and similarly, anyone testing negative does not have the virus (at the time of testing).

Now we can say that people with a positive test have been exposed to the virus at some point leading up to the test, but we don’t know exactly when they contracted the virus. Therefore, they are left-censored, since the event is when the individual contracted the virus, not the positive test. Similarly, anyone who tests negative is right-censored. In this rather unique case, our dataset is filled with only left and right censored cases, we actually never observe the event directly and only have lower and upper bounds for individuals’ time of contracting the virus.
In reality, the situation becomes even more complex given the testing accuracy, and we would need to consider interval censoring as well.
Conversely, if we define the event as the positive test then we have no left censoring and have the case as described previously, observing the event and all negative tests are then right censored, as shown in the diagram below.
How does this relate to turnover?
As much as virus outbreaks and clinical trials are relevant today, it is not immediately clear how this translates to turnover. In actuality it is basically the same process except for a few things.
- Firstly, we can ignore left censoring, as it is irrelevant for churn – we know when an employee leaves the company, and we only deal with right censoring – employees still present at the company.
- Secondly, and most importantly, in the cases above we start observing our participants/population all at the same time, t0, which we can set to zero for convenience. However, time does not have to be an absolute measure and it can instead be relative, by using a time duration. In this case, individuals can start at different times relative to each other, but we measure the time difference between each individual’s start and end dates. Again, this is relevant for the case of turnover since this is the definition of tenure.
Let me illustrate this with an equivalent example as the medical study but this time for turnover.
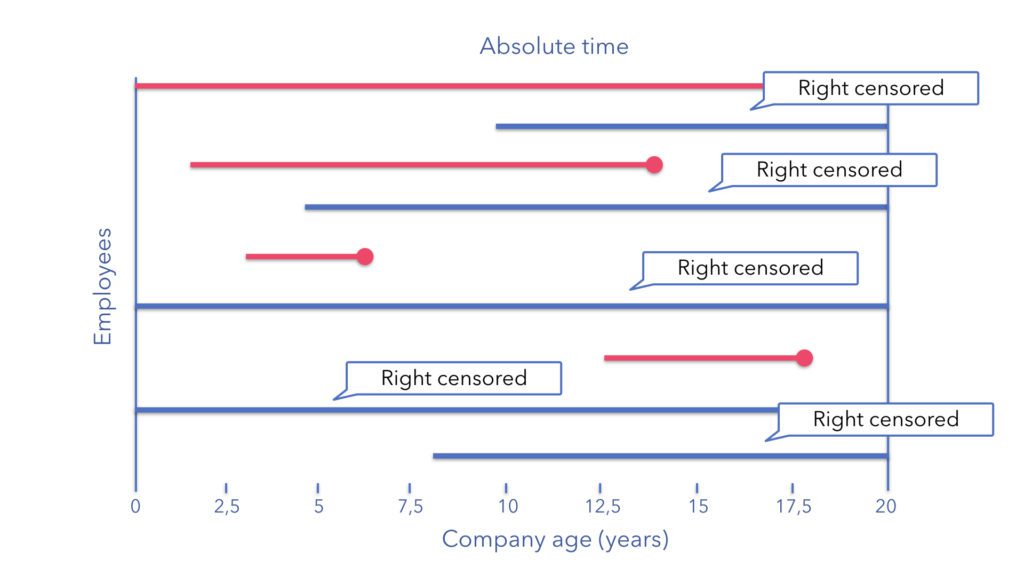
This diagram represents absolute time (the date and year the company was founded until the present day). Employees join and leave the company at different times (which is how it works in reality).
We can see that the company has just reached its 20 year anniversary but unfortunately one of the founders left a year before this landmark (top red line). We also notice that other employees come and go during the 20 years with some new starters still present at the company. The company, therefore, started with 3 employees (founders), currently has 5 employees still present, and has had a total of 9 over its entire history (not the biggest company in the world). The maximum possible tenure is held by two of the founders at 20 years.
In this example, anyone still present at the company at their 20-year anniversary party has been right-censored, while people who left before (and missed a great party) are not censored and we observe the “death” event.
Now, we can translate the previous diagram, which is measured in absolute time, into a slightly different representation, instead taking our time measure as relative – which we understand as tenure.
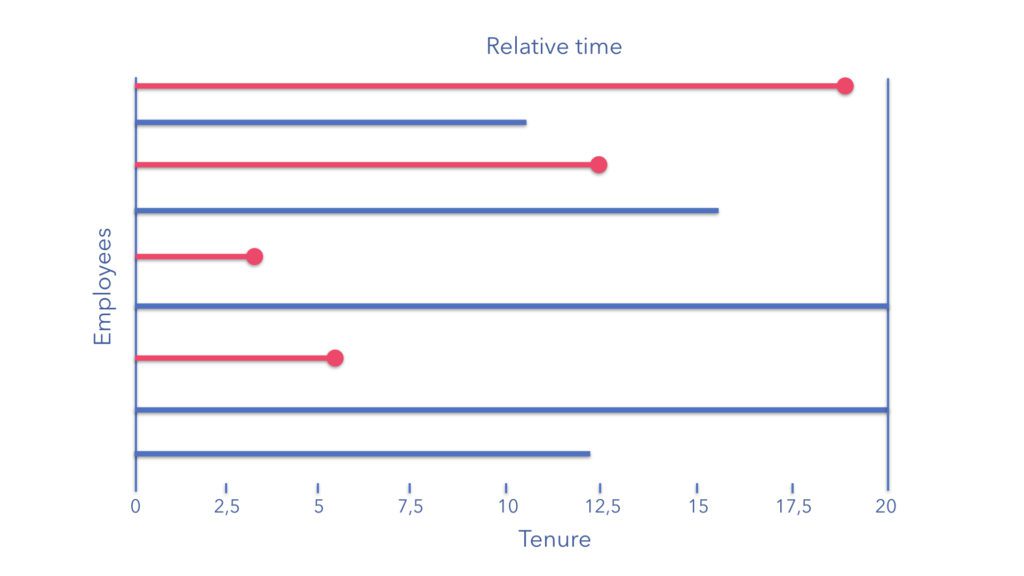
Using tenure instead of company age as our x-axis then allows us to apply survival analysis to turnover whilst taking into account right censoring!
That concludes part 2 of the series on survival analysis. I hope by now I am starting to convince you that this old school method is not too bad 😉



